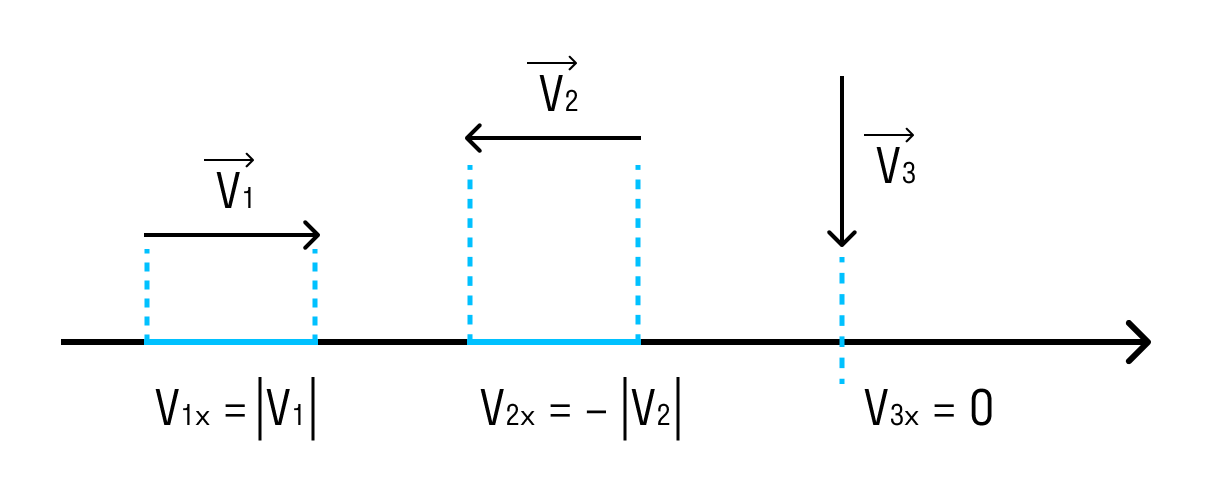Формула момента силы

Мощность двигателя — как работает и что это такое,на что влияет

Изобретенный более 100 лет назад поршневой двигатель внутреннего сгорания (ДВС), на сегодняшний день все еще является самым распространенным в автомобилестроении. При выборе модели двигателя своего будущего автомобиля покупатель может предварительно ознакомиться с его основными характеристиками. В этой статье мы подробно расскажем об основных показателях двигателей внутреннего сгорания, что они собой представляют и как влияют на работу.

Важнейшими характеристиками двигателя являются его мощность, крутящий момент и обороты, при которых эта мощность и крутящий момент достигаются.

Обороты двигателя

Под широкоупотребимым термином «обороты двигателя» имеется в виду количество оборотов коленчатого вала в единицу времени (в минуту).

И мощность, и крутящий момент — величины не постоянные, они имеют сложную зависимость от оборотов двигателя. Эта зависимость для каждого двигателя выражается графиками, подобными нижеследующему:

Производители двигателей борются за то, чтобы максимальный крутящий момент двигатель развивал в как можно более широком диапазоне оборотов («полка крутящего момента была шире»), а максимальная мощность достигалась при оборотах, максимально приближенных к этой полке.

Мощность двигателя

Чем выше мощность, тем большую скорость развивает авто

Мощность — это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. При вращательном движении мощность определяется как произведение крутящего момента на угловую скорость вращения.

Мощность двигателя последнее время все чаще указывают в кВт, а ранее традиционно указывали в лошадиных силах.

Как видно на приведенном выше графике, максимальная мощность и максимальный крутящий момент достигаются при различных оборотах коленвала. Максимальная мощность у бензиновых двигателей обычно достигается при 5-6 тыс. оборотов в минуту, у дизельных — при 3-4 тыс. оборотов в минуту.

График мощности для дизельного двигателя:

Крутящий момент

Крутящий момент характеризует способность ускоряться и преодолевать препятствия

Крутящий момент (момент силы) — это произведение силы на плечо рычага. В случае кривошипно-шатунного механизма, данной силой является сила, передаваемая через шатун, а рычагом — кривошип коленчатого вала. Единица измерения — Ньютон-метр.

Иными словами, крутящий момент характеризует силу, с которой будет вращаться коленвал, и насколько успешно он будет преодолевать сопротивление вращению.

На практике высокий крутящий момент двигателя будет особенно заметен при разгонах и при передвижении по бездорожью: на скорости машина легче ускоряется, а вне дорог — двигатель выдерживает нагрузки и не глохнет.

Виды мощности

Для определения характеристик двигателя применяют такие понятия мощности как:

Индикаторной называют мощность, с которой газы давят на поршень. То есть, не учитываются никакие другие факторы, а только давление газов в момент их сгорания. Эффективная мощность, эта та сила, которая передается коленчатому валу и трансмиссии. Индикаторная будет пропорциональной литражу двигателя и среднему давлению газов на поршень.

Также есть параметр, называемый литровой мощность двигателя. Это соотношение объема двигателя к его максимальной мощности. Для бензиновых моторов литровая мощность составляет в среднем 30-45 кВт/л, а у дизельных – 10-15 кВт/л.

Как узнать мощность двигателя автомобиля

Можно посмотреть в документах на машину, но иногда требуется узнать мощность автомобиля, который подвергался тюнингу или давно находится в эксплуатации. В таких случаях не обойтись без динамометрического стенда. Его можно найти в специализированных организациях и на станциях техобслуживания. Колеса автомобиля помещаются между барабанами, создающими сопротивление вращению. Далее имитируется движение с разной нагрузкой. Компьютер сам определит мощность двигателя. Для более точного результата может понадобиться несколько попыток.

Примеры решения задач

Пример

Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.

Решение. За основу решения задачи примем формулу, определяющую момент силы:

$$\bar{M}=\bar{r} \times \bar{F}(1.1)$$

В векторном произведении (видно из рисунка) $\bar{r} \neq 0, \bar{F} \neq 0$ . Угол между вектором силы и радиус –
вектором также будет отличен от нуля (или $180^{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.

Ответ. $\bar{M} \neq 0$

Слишком сложно?

Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2.
В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?

Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:

$$M=I \varepsilon(2.1)$$

где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:

$$\varepsilon=\frac{d \omega}{d t}(2.2)$$

Перепишем (2.1), используя (2.2), имеем:

$$M=I \frac{d \omega}{d t}(2.3)$$

Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.

Ответ. M=0 в точке 3.

Читать дальше: Формула мощности.

Преобразование единиц измерения. Таблицы пересчета физических величин

Длина

Формула средней скорости 1 дюйм	= 2,54 см	1 миллиметр	= 0,03937 дюйма
1 фут	= 0,3048 м	1 сантиметр	= 0,3937 дюйма
1 ярд	= 0,9144 м	1 дециметр	= 0,3281 фута
1 род	= 5,0292 м	1 метр	= 3,281 фута
1 чейн	= 20,117 м	1 метр	= 1,094 ярда
1 фурлонг	= 201,17 м	1 декаметр	= 10,94 ярда
1 миля	= 1,6093 м	1 километр	= 0,6214 мили
1 морская миля	= 1,8532 м	1 километр	= 0,539 морской мили

Площадь

1 кв. дюйм	= 6,4516 кв. см	1 кв. сантиметр	= 0,1550 кв. дюйма
1 кв. фут	= 929,03 кв. см	1 кв. метр	= 1,550 кв. дюйма
1 кв. ярд	= 0,8361 кв. м	1 ар	= 119,60 кв. ярда
1 акр	= 4046,9 кв. м	1 гектар	= 2,4711 акра
1 кв. миля	= 259,0 га	1 кв. километр	= 0,3861 кв. мили

Объем

1 куб. дюйм	= 16,387 куб. см	1 куб. сантиметр	= 0,061 куб. дюйма
1 куб. фут	= 0,0283 куб. м	1 куб. дециметр	= 0,035 куб. фута
1 куб. ярд	= 0,7646 куб. м	1 куб. метр	= 1,308 куб. ярда

Меры сыпучих тел и жидкостей

Британия	США
1 пинта	= 0,5506 л	1 пинта	= 0,473 л
1 кварта	= 1,136 л	1 кварта	= 0,9463 л
1 галлон	= 4,546 л	1 галлон	= 3,785 л
1 пек	= 9,092 л	1 пек	= 8,809 л
1 бушель	= 36,369 л	1 бушель	= 35,24 л

Энергия, тепло, работа

Единица измерения энергии	Эквивалентные единицы
кДж	ккал	кВт ч	кГс м
кДж	1	0,239	0,00278	102,0
ккал	4,19	1	0,00116	427
кВт ч	3600	860	1	367200
кГс м	0,00981	0,00234	2,72 х 106	1

Давление

Пересчет	В
Па (Паскаль)	Бар (Бар)	мм рт. ст. (миллиметр ртутного столба)	мм вод. ст. (миллиметр водяного столба)	кгс/см2 (техническая атмосфера)	атм (физическая атмосфера)
Из	1 Па	1	10-5	7,5 10-3	0,102	1,02 10-5	0,99 10-5
1 бар	105	1	750,1	10 200	1,02	0,987
1 мм рт. ст.	133	13,33 10-4	1	13,6	0,00136	0,001316
1 мм вод. ст.	9,81	0,9806 10-4	0,07355	1	0,0001	9,68 10-5
1 кгс/см2	98 100	0,9807	735,6	10 000	1	0,968
1 атм	101 300	1,013	760	10 330	1,033	1

 ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Общероссийский классификатор единиц измерения (ОКЕИ) ОК 015-94 (МК 002-97)

Калькулятор перевода единиц измерения физических величин

Знак момента силы

Тангенциальная составляющая силы, входящая в формулу момента силы, может иметь два направления. В зависимости от направления такой момент силы может как увеличивать скорость вращения тела, так и уменьшать ее.

Для учета этой разницы вводится такое свойство момента, как знак.

Поскольку угол на координатной плоскости отсчитывается в направлении против часовой стрелки, то момент силы, поворачивающий тело в этом направлении, считается положительным. Если момент силы поворачивает тело по часовой стрелке, он принимается отрицательным.

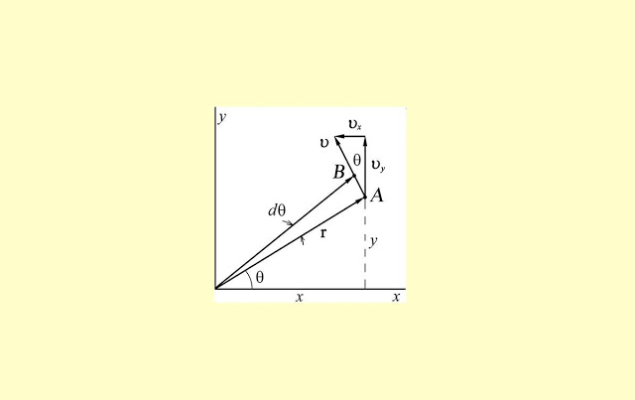
Рис. 3. Угол поворота.

Что мы узнали?

Для вращательного движения особую роль играет точка приложения силы. Поэтому при исследовании вращательного движения используется не понятие силы, а понятие момента силы, который равен произведению тангенциальной составляющей силы на радиус поворота и измеряется в ньютон-метрах.

Тест по теме

1. Вопрос 1 из 10

   При вращательном движении, в отличие от поступательного:

   • все точки тела имеют одинаковую скорость
   • все точки тела находятся в покое
   • различные точки имеют разную скорость
   • различные точки имеют одну из двух скоростей

Начать тест(новая вкладка)

Крутящий момент

Читая характеристики двигателя той или иной модели, мы встречаем такие понятия:

• мощность — лошадиные силы;
• максимальный крутящий момент — Ньютон/метры;
• обороты в минуту.

Люди, увидев значение 100 или 200 лошадиных сил, полагают, что это очень хорошо. И они правы — 200 лошадиных сил для мощного кроссовера или 100 л.с. для компактного городского хетчбэка действительно неплохие показатели

Но нужно обращать внимание также на максимальный крутящий момент и обороты двигателя, поскольку такая мощность достигается на пике работы двигателя

Говоря простым языком, максимальную мощность в 100 л.с. ваш двигатель может развить при определенных оборотах двигателя. Если же вы ездите по городу, а стрелка тахометра показывает 2000-2500 оборотов, тогда как максимум составляет 4-5-6 тысяч, то в данный момент используется лишь часть этой мощности — 50 или 60 лошадиных сил. Соответственно и скорость будет небольшая.

Если же вам нужно перейти на более быстрый режим движения — выехали на скоростную трассу или хотите обогнать фуру — вам нужно увеличить количество оборотов, тем самым увеличив скорость.

Другой пример — вы едете по трассе, на большой скорости на 4-5 передаче. Если же дорога начинает подниматься в гору и уклон довольно ощутимый, то мощности двигателя может просто не хватить. Поэтому приходится переключаться на пониженные передачи, при этом выжимая большую мощность с двигателя. Крутящий момент в данном случае служит для увеличения мощности и помогает активизировать все силы вашего двигателя на преодоление препятствия.

Наибольший крутящий момент выдают бензиновые двигатели — при 3500-6000 оборотов в минуту в зависимости от марки автомобиля. У дизельных моторов максимальный крутящий момент наблюдается при 3-4 тысячах оборотов. Соответственно, у дизельных автомобилей динамика разгона лучше, им проще быстро разгоняться и выжимать всех «лошадей» с мотора.

Однако, по максимальной мощности они проигрывают своим бензиновым собратьям, поскольку при 6000 оборотах мощность у бензинового автомобиля может достигать нескольких сотен лошадиных сил. Не зря ведь все самые быстрые и мощные автомобили, о которых мы писали на Vodi.su ранее, работают исключительно на высокооктановом бензине А-110.

Ну и чтоб стало совсем понятно, что такое крутящий момент, нужно посмотреть на единицы его измерения: Ньютоны на метры. Говоря простым языком, это сила с которой мощность передается от поршня через шатуны и коленчатый вал на маховик. А уже от маховика эта сила передается на трансмиссию — коробку передач и от нее на колеса. Чем быстрее движется поршень, тем быстрее вращается маховик.

Отсюда приходим к выводу, что мощность двигателя производит крутящий момент. Есть техника, в которой максимальная тяга вырабатывается на низких оборотах — 1500-2000 об/мин. Действительно, в тракторах, самосвалах или внедорожниках мы прежде всего ценим мощность — водителю джипа некогда раскручивать коленвал до 6-ти тысяч оборотов, чтобы выехать из ямы. То же самое можно сказать о тракторе, который тянет тяжелую дисковую борону или трехкорпусный плуг — максимальная мощность нужна ему на малых оборотах.

От чего зависит крутящий момент

Понятно, что самые мощные моторы обладают самым большим объемом. Если у вас какая-нибудь малолитражка типа Daewoo Nexia 1.5L или компактный хетчбэк Hyundai i10 1.1L, то резко разогнаться или стартовать с места с пробуксовкой вряд ли получится, хотя умение правильно переключать передачи и использовать всю мощь мотора делает свое дело.

Эластичность двигателя — это важный параметр, говорящий о том, что соотношение мощности и количества оборотов оптимальное. Можно ехать на пониженных передачах с довольно большой скоростью, выжимая при этом максимум с двигателя. Это очень хорошее качество как для городского режима езды, где нужно постоянно тормозить, разгоняться и снова останавливаться, — так и для трассы — одним нажатием на педаль можно разогнать двигатель до высоких оборотов.

Крутящий момент — один из самых важных параметров двигателя

Таким образом мы приходим к выводу, что все параметры двигателя тесно связаны между собой: мощность, крутящий момент, количество оборотов в минуту, при которых достигается максимальный крутящий момент.

Крутящий момент является той силой, которая помогает полностью использовать всю мощь двигателя. Ну а чем больше мощность мотора, тем больше крутящий момент. Если же он еще и достигается на невысоких оборотах, то на такой машине можно будет легко разогнаться с места, или взобраться на любую горку, не переходя на пониженные передачи.

На этом видео прекрасно разобрали что такое крутящий момент и лошадиные силы.

(12 оценок, среднее: 4,75 из 5)

Направление момента силы и его знак

Момент силы рассчитывают относительно точки, где он представляет собой вектор, или относительно оси, где есть лишь проекция вектора на ось.

Итак, берем точку Q — полюс, относительно которой рассчитывается момент силы. Далее следует провести радиус-вектор r из Q к F — точке приложения. Далее категория рассчитывается так:

\(M=\lbrack rF\rbrack\)

В результате получается вектор, длина которого определяется модулем:

\(\vert M\vert=\vert r\vert\ast\vert F\vert\ast\sin\varphi\)

Здесь φ является углом между векторами r и F.

Вектор М направлен так, что векторы r, F, M — правые. Это можно определить следующим образом. Ваше территориальное нахождение — на конце 3-го вектора, а на другие два направлен взгляд. Если самый короткий переход от вектора 1 к вектору 2 происходит против часовой стрелки, то они являются тройкой правых векторов. Если наоборот, т.е. по часовой стрелке, то они считаются левыми.

Затем следует совместить начала r и F путем параллельного переноса вектора F в Q. Через точку Q нужно провести ось перпендикулярно r и F. Возможны 2 направления — вниз или вверх.

Далее изобразите стрелку вектора на оси вверх. Оттуда посмотрите на направления r и F. Переход от одного вектора к другому также обозначьте стрелкой. Если стрелка указывает направление против часовой стрелки, то тройка векторов — правая. Это означает, что выбранное направление верно. В противном случае его необходимо сменить на противоположное.

Примечание

Правило правой руки определяет направление момента силы. Указательный палец совмещается с радиус-вектором, а средний — с вектором силы

От конца большого пальца, направленного вверх, обратите внимание на оба вектора: при переходе от указательного к среднему происходит против часовой стрелки направление момента силы аналогично направлению, показанному большим пальцем; переход против часовой говорит о противоположном направлении

Что касается знака, то момент силы относительно любой точки имеет знак:

• по направлению часовой стрелки — минус (-);
• против направления часовой стрелки — плюс (+).

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

График крутящего момента

Пример №1. Суперкар мощностью 500 сил с крутящим моментом двигателя 500 Н*м и магистральная фура-тягач с отдачей 500 сил и 2500 Н*м на колесах тем не менее имеют абсолютно равный крутящий момент при движении с одинаковой скоростью на оборотах максимальной мощности: М (момент на колесах, приводящий машины в движение) = N (мощность двигателя) / n (обороты колеса, при условии, что у суперкара и фуры они одинакового диаметра).

Вывод: цифра мощности отражает тягу и динамику автомобиля, а цифра крутящего момента двигателя, не учавствующая в вычислениях, может быть любой и не имеет значения.

Пример №2. Зайдем с другой стороны. Тот же суперкар и фура с вышеуказанными характеристиками (аналоги Porsche 911 GT3 RS 4.0, Scania R500 и многие другие суперкары и грузовики), как правило, имеют максимальные обороты двигателя около 9000 и 1800 соответственно. Для того чтобы компенсировать пятикратную разницу в оборотах (иметь ту же скорость движения), на фуре придется применять в пять раз более «длинную» трансмиссию, которая, соответственно, будет передавать в 5 раз меньше момента на колеса: 2500 Н*м делим на 5 и получаем те же 500 Н*м (приведенный момент), как в суперкаре.

Вывод: мы получили то же равенство тягово-динамического потенциала машин равной мощности, что и в примере №1.

В представленной таблице крутящего момента двигателей цифры Нм приведены к величине 7000 об/мин.

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

|OA|=FB/FA)*|OB|=30/80*80=30 см

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

4T = 4*100= 400 Н

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

mg=F*5/0,8=120*5/0,8=750Н

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Ловите момент! Запишите ребенка на бесплатный вводный урок в современную школу Skysmart: покажем, как у нас все устроено, определим план развития и влюбим в науку!

Момент силы

В динамике вращательного движения важна не непосредственно величина силы, а произведение этой величины на расстояние от точки вращения. Это произведение называется моментом силы, обозначается буквой $M$:

$$M=F_\tau R$$

Из приведенной формулы можно получить размерность момента: поскольку сила измеряется в ньютонах, а радиус — в метрах, единица измерения момента силы получается равной ньютон-метру. Радиус вращения при этом нередко называют «плечом силы» $l$.

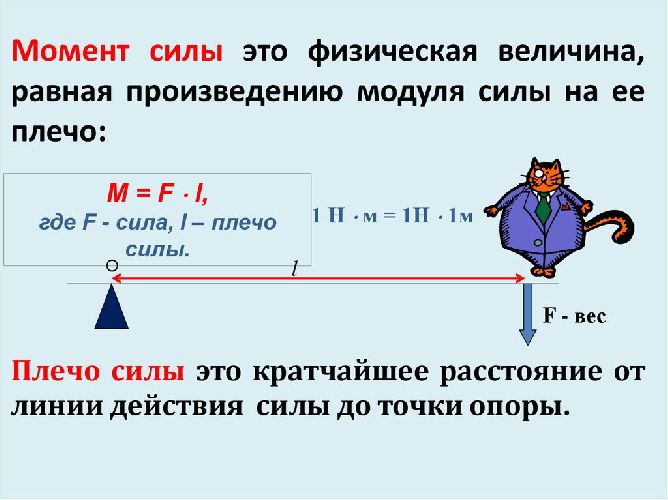
Рис. 2. Момент силы.

Обратите внимание, что вращательное движение создает только компонента силы, направленная перпендикулярно радиусу поворота, — тангенциальная составляющая силы:

$$F_\tau = F sin \alpha,$$

где $\alpha$ — это угол между радиус-вектором точки, к которой приложена сила $F$, и вектором приложения этой силы.

В самом деле, если сила направлена от точки приложения точно в сторону оси вращения, никакого вращательного движения создать с помощью этой силы не получится, какой бы модуль у этой силы не был. Формула также подтверждает это — синус угла между вектором силы, направленной точно на ось, и радиус-вектором точки приложения равен нулю, а значит, и тангенциальная составляющая силы также будет равна нулю. Момент такой силы, соответственно, также будет нулевым. Создать вращение будет невозможно.

Вращение невозможно создать также в случае, когда сила приложена непосредственно к оси вращения, независимо от ее направления. Радиус-вектор точки приложения силы при этом равен нулю, и определить тангенциальную составляющую приложенной силы невозможно. Момент такой силы оказывается нулевым.

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.