Формула нахождения значений скорости, времени и расстояния

Средняя квадратичная скорость молекул газа — что это за параметр

Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.

Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.

Определение

Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве  модели окружающих нас газов, например, обычного воздуха.

Определение

Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.

Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.

В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».

Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.

Виды ходьбы

Скандинавская

Другое название метода — финская ходьба ( Nordic Walking ), впервые описана финскими специалистами по тренировке лыжников в летний период. Этот метод требует особой экипировки — подходящей обуви и палок, наподобие лыжных, однако более коротких и тяжелых. Ходьба с палками подразумевает дополнительную нагрузку для мышц рук и верхней части туловища и более широкую амплитудность движений. Специальная конструкция креплений в виде перчаток с обрезанными пальцами позволяет не сжимать ручку палки, а как бы опираться на нее и помогает отталкиваться от земли. Палки подбираются индивидуально и составляют около 66-68 % от роста тренирующегося. Использование палок позволяет более функционально распределить нагрузку на позвоночник и суставы конечностей, риск травмы минимален. Скорость движения может быть разной — от легкого прогулочного шага до почти бега, в среднем — 6 км/ч.

Оздоровительная

Этот способ предполагает увеличение скорости до 6-8 км/ч, почти вдвое быстрее, чем при обычной ходьбе. В таком темпе необходимо идти от 30 до 60 минут, не сбавляя шага. В целом такая скорость позволяет разговаривать, не сбивая дыхание. Эта ходьба максимально приближена к пределу физиологических возможностей человека, у нее нет специальной техники выполнения. Для людей, имеющих лишний вес, перенесших травмы и операции, очень полезной будет и обычная скорость движения, главное — идти без остановок хотя бы полчаса.

Спортивная

Олимпийский вид спорта, скорость движения при ней от 7 до 15 (17) км/ч. Его отличие от других способов хождения в том, что контакт ног с землей должен быть видимым и постоянным, а нога, вынесенная вперед, не сгибается в колене. Вторая нога ставится на землю раньше, чем оторвется первая, каждый шаг является «двухопорным». Это формирует специфическую «походку», которая забавно выглядит со стороны, но она наименее травматична из-за мягкой постановки стопы. Руки согнуты в локтях и энергично работают на уровне грудной клетки, что позволяет включить в работу практически все мышцы тела. Необходима специальная обувь, которая будет анатомически поддерживать свод стопы, иначе возможно возникновение болей. Также требуется оборудованная ровная трасса без препятствий и дефектов.

Энергетическая

Некоторые источники описывают этот метод как «индейскую походку», он направлен не на уникальные физические достижения, а на целительный психологический эффект. Метод впервые описан в книгах Карлоса Кастанеды , который вел антропологические исследования индейских племен. Суть ее заключается в том, чтобы идти друг за другом, фокусируясь на ногах впереди идущего или на земле перед собой. Идти необходимо молча, сосредоточенно, достаточно долго и монотонно. Это помогает достичь трансового состояния и «остановки внутреннего диалога», то есть бесконечного потока мыслей. Руки должны быть абсолютно свободны, возможно дополнительное утяжеление в виде рюкзака. Энергетическая ходьба дает полноценный медитативный эффект и хорошо заряжает тренирующегося.

Формула мгновенной скорости

Определение

Мгновенная скорость (обычно просто скорость) — это векторная величина, равная первой производной от радиус-вектора ($\overline{r}$), определяющего положение движущейся материальной точки, по времени ($t$):

\

Представим вектор $\overline{r}$ в декартовой системе координат в виде:

где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:

Проекциями вектора скорости на оси координат X, Y,Z являются:

Величину (модуль) скорости найдем в соответствии с формулой:

Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус — вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:

в таком случае в формуле (1) $\overline{r}\left(t\right)$ будем рассматривать как сложную функцию: $\overline{r}\left$, формулой скорости станет:

Величина $\Delta s$ — это расстояние между двумя точками по траектории движения тела. Модуль $\left|\Delta \overline{r}\right|$ — расстояние между этими точками по кратчайшему направлению — прямой. При сближении рассматриваемых двух точек разница между $\Delta s$ и $\left|\Delta \overline{r}\right|$ уменьшается. Имеем:

где $\overline{\tau \ }$ — единичный вектор, касательный к траектории движения материальной точки. Кроме этого:

модуль скорости движения точки по траектории. Уравнение (6) представим как:

Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).

Примеры решения задач

Пример

Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v₁, остальную часть пути данная точка 1/2 времени двигалась со скоростью v₂, последний
участок пути точка двигалась со скоростью v₃.

Решение. В качестве основы для решения задачи формулу:

$$\langle v\rangle=\frac{s}{\Delta t}(1.1)$$

где время потраченное на путь ($\Delta t$) делится на три части:

$$\Delta t=t_{1}+t_{2}+t_{3}(1.2)$$

При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:

$$\left\{\begin{array}{c}\frac{1}{2} s=v_{1} t_{1} \rightarrow t_{1}=\frac{s}{2 v_{1}} \\ \frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} \rightarrow t_{3}=\frac{s}{2\left(v_{2}+v_{3}\right)}(1.3) \\ t_{2}=t_{3}=\frac{1}{2} t\end{array}\right.$$
$$\langle v\rangle=\frac{2 v_{1}\left(v_{2}+v_{3}\right)}{v_{2}+v_{3}+2 v_{1}}$$

Ответ. $\langle v\rangle=\frac{2 v_{1}\left(v_{2}+v_{3}\right)}{v_{2}+v_{3}+2 v_{1}}$

Слишком сложно?

Формула средней скорости не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые
s метров пути, если функция скорости задана уравнением: $v=A \sqrt{x}$,
где A=const>0. Считать, что x=0 при t=0.

Решение. Сделаем рисунок.

В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное,
то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:

$$\langle v\rangle(t+\Delta t)=\frac{\Delta x}{\Delta t}(2.1)$$

По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:

$$\langle v\rangle=\frac{s}{t}(2.2)$$

Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:

$$v=\frac{d x}{d t}=A \sqrt{x}(2.3)$$

Выразим из (2.2) x:

$$\frac{d x}{\sqrt{x}}=A d t \rightarrow x=\frac{A^{2} t^{2}}{4}(2.4)$$

Так как движение происходит по оси X, то $x=s=\frac{A^{2} t^{2}}{4}$ . Выразим время, которое точка затратила на путьs :

$$t=\frac{2 \sqrt{s}}{A}(2.5)$$

Подставим время из (2.4) в формулу (2.2):

$$\langle v\rangle=\frac{A}{2} \sqrt{s}$$

Ответ. $\langle v\rangle=\frac{A}{2} \sqrt{s}$

Читать дальше: Формула угловой скорости.

Наука и скорость бега

Ученые утверждают, что человек способен бежать со скоростью почти 65 км/ч. Новое исследование американских учёных о биологических пределах скорости предлагает по-новому посмотреть на биологию скорости человека.

Считается, что скорость ограничена силой, с которой конечности могут ударяться о поверхность во время бега. Элитные спортсмены могут прикладывать от 360 до 456 кг на одну конечность во время каждого шага. С такими цифрами легко поверить, что они бегут на пике своих возможностей. Но учёные выяснили, что это не так. Что конечности способны прикладывать гораздо большие силы к поверхности.

Ответ кроется в периодах времени контакта стопы с землёй. У элитных спринтеров это время составляет менее одной десятой секунды, а пиковые значения составляют менее одной двадцатой секунды.

Для исследования учёные использовали высокоскоростную беговую дорожку, развивающую скорость более 65 км/ч и способную измерять силу каждого шага. На ней спортсмены бежали назад, вперёд, прыгали на одной ноге. Оказалось, что во время прыжков на одной ноге на максимальной скорости сила, приложенная к поверхности, больше силы при беге на максимальной скорости на двух ногах на 30%.

Также выяснилось, что время соприкосновения ноги с поверхностью при беге вперёд совпадает во временем соприкосновения конечности при беге назад, при этом бег назад, конечно, медленнее. Это совпадение времени при двух очень разных видах активности указывает, насколько быстро мышечные волокна могут создавать силы, необходимые для того, чтобы бегун отрывался от земли во время каждого шага.

Новая работа показывает, что ограничения скорости бега устанавливаются ограничениями скорости сокращения самих мышечных волокон, а скорость сокращения волокон устанавливает предел того, насколько быстро конечность бегуна может прикладывать силу к поверхности бега.

Чтобы преодолеть биологические ограничения скорости, учёные из Гарварда придумали экзокостюм, который снижает метаболические затраты на бег и повышает мышечную производительность. Этот костюм лёгкий и плотно облегает тело. Он имеет приводной блок, который тянет за провода, выступающие в роли второй пары мышц-разгибателей бедра. Исследование показало, что помогая мышцам бедра, костюм влияет и на разгибание колена, и на прикладываемую ступнёй силу к поверхности.

На данный момент исследования продолжаются, чтобы ещё больше снизить метаболические затраты на бег. Еще один немаловажный аспект – доступность такого экзокостюма. Цель учёных – разработать портативную систему, чтобы польза от неё значительно снижала стоимость её ношения.

Есть версия, что скорость бега человека ограничена, потому что большую часть времени бега мы находимся в воздухе. А когда наши ноги касаются земли, у нас остается слишком мало времени, чтобы приложить силу к поверхности. Так, Усэйн Болт находится на земле 42-43% от общего времени шага, в то время как самые быстрые животные – гепард или лошадь – тратят две трети времени шага на контакт с землёй. Неужели, чтобы бежать быстрее, стоит бежать на четырех ногах?

Мировой рекорд Гиннесса для человека, бегущего 100 метров на четвереньках, улучшился с 18,58 секунды в 2008 году (первый год отслеживания записи) до 15,71 секунды в 2015 году. Исследователи сделали вывод на основе этих цифр, что к 2048 году человек на четвереньках сможет двигаться быстрее, чем человек, бегущий прямо!

Для чего это нужно?

Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.

Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.

Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.

Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи » » и » » . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.

Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:

Если участков пути было два, тогда

Если три, то соответственно:

*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.

Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:

Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

Таким образом

Решите самостоятельно:

Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трёх участках пути. СК будем искать по формуле:

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

Вычисляем скорость:

Решите самостоятельно:

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Сказано о трёх участках пути. Формула:

Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:

Решите самостоятельно:

Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Уровень B

1 . О какой скорости – средней или мгновенной – идет речь в следующих случаях:

а) пуля вылетает из винтовки со скоростью 800 м/с;

б) скорость движения Земли вокруг Солнца 30 км/с;

в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;

г) мимо вас проехал автомобиль со скоростью 72 км/ч;

д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?

2 . Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?

3 . Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.

4 . На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?

5 . Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.

6 . Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.

7 . Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.

8 . Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.

9 . Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.

10 . Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.

11 . Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.

12 . Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

V ср = S/t.

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

v=v+at.

Здесь v — начальная скорость тела, a=const — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

​​​​​​​

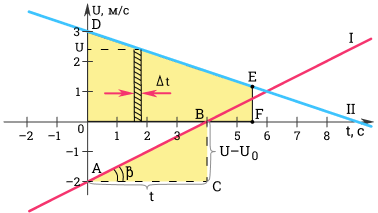
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a=v-vt=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v=-2 мс; a=,5 мс2.

Для второго графика: v=3 мс; a=-13 мс2.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

По данному графику можно также вычислить перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v+v2t=2v+(v-v)2t.

Мы знаем, что v-v=at, поэтому окончательная формула для перемещения тела примет вид:

s=vt+at22

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Частные случаи нахождения средней скорости

Это задачи на нахождение средней скорости

Задачи простые, важно понять и запомнить формулу: Если участков пути было два, тогда Если три, то соответственно: *Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в числители суммируем расстояния пройденные за соответствующие им отрезки времени. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61 км/ч, а вторую половину времени – со скоростью 87 км/ч

В правительстве обращение пока не комментируют. Ограничить скорость в населенных пунктах во вторник попросили премьера глава комитета Совета Федерации по регламенту и организации парламентской деятельности Вадим Тюльпанов и член этого комитета, экс-глава ГАИ России Владимир Федоров. Авторы обращения уверены, что снижение разрешенного лимита с 60 до 50 км/ч позволит сократить количество ДТП и уровень смертности на дорогах, а также поспособствует

. Подробнее: «По оценке экспертов, при скорости автомобиля 50 км/ч с учетом времени реакции и тормозного пути расстояние, которое проходит автомобиль до остановки, составляет 28 метров, а при скорости 60 км/ч — 36.

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

• Пусть — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени . Аналогично, на втором участке пути тело двигалось в течение интервала времени .
• Тогда средняя скорость движения равна:

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

• Пусть — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: .
• Тогда средняя скорость движения равна:

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-ЗападнойСергей Валерьевич